프로그램 개요 :
C 언어를 사용한 크러스컬 알고리즘(Kruskal Algorithm) 구현.
- 붕괴법칙을 적용하지 않은 크러스컬 알고리즘.
- 붕괴법칙을 적용한 크러스컬 알고리즘
크러스컬 알고리즘에 대한 설명은 아래 링크의 이전 글에서 볼 수 있습니다.
2020.07.02 - [알고리즘] - 크러스컬(Kruskal) 알고리즘
크러스컬(Kruskal) 알고리즘
크러스컬(Kruskal) 알고리즘이란? 크러스컬 알고리즘은 최소 비용 신장 그래프를 찾는 알고리즘 입니다. 변의 개수를 E, 꼭지점의 개수를 V라고 한다면 크러스컬 알고리즘은 O(ElogV)의 시간 복잡도
sobamemil.tistory.com
이 글에서는 예로 주어진 그래프에 대해서 크러스컬 알고리즘으로 문제를 해결하는 방법과 코드를 작성하였습니다.
입력 가중치 그래프 :
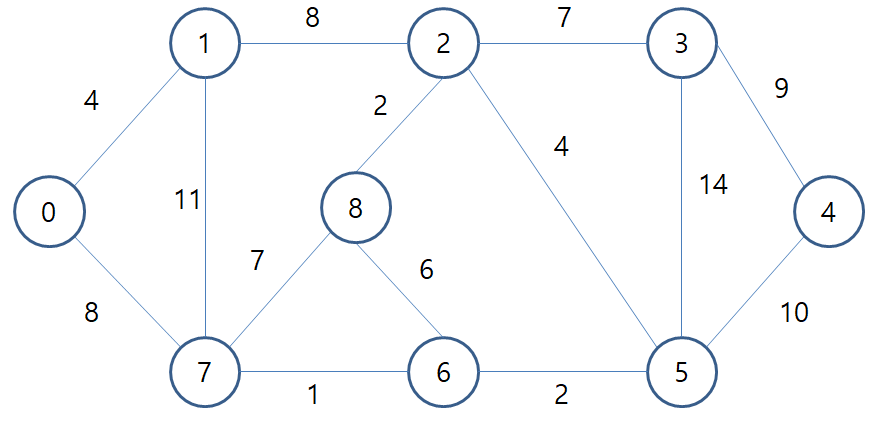
입력 파일 :
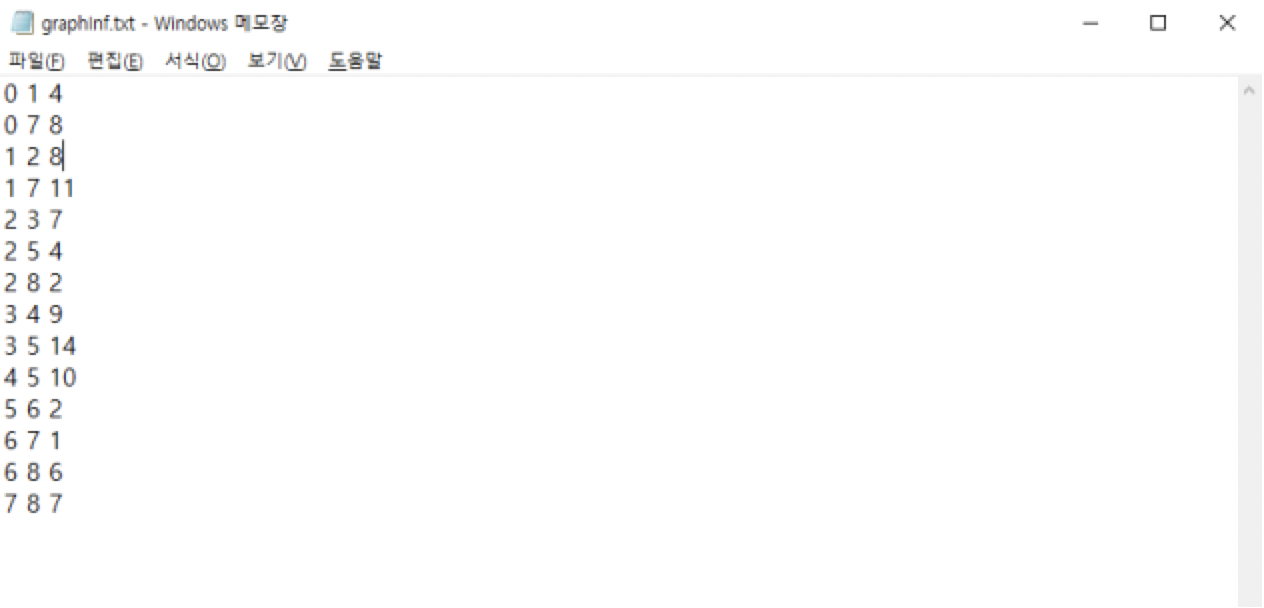
입력 데이터가 들어있는 .txt 파일입니다.
프로그램 실행 결과 :
붕괴법칙을 적용하지 않은 경우
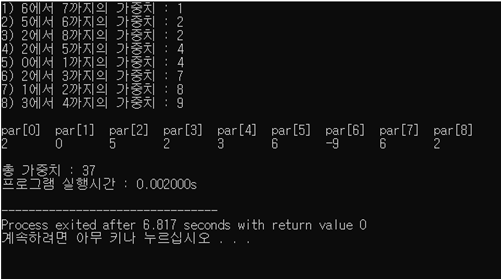
프로그램 구조 및 설계:
총 1개의 구조체와 main() 함수를 포함한 9개의 함수로 이루어져 있음.
struct Graph : 정점 u를 나타내는 int x와 정점 v를 나타내는 int y 그리고 가중치를 나타내는 int wei 변수를 가지고 있음.
int main() 함수 : clock_t 타입의 변수를 선언하고 clock() 함수를 이용해 크러스컬 알고리즘의 실행 시간 측정, FILE 타입의 포인터 fp를 선언하고 fopen() 함수를 통해 입력 파일을 오픈, 비용 인접 행렬을 만드는 함수 호출, 크러스컬 알고리즘을 실행하는 함수 호출 등의 역할을 함.
int compare(struct Graph *g1, struct Graph *g2) 함수 : C언어에서 제공하는 정렬 함수인 qsort() 함수를 사용할 때 특정 값을 비교해서 결과에 따른 값을 리턴해주기 위한 함수. 이 프로그램에서는 구조체 Graph의 변수 wei 즉, 가중치를 비교해 값을 리턴.
void readFileMakeGraph(FILE *fp) 함수 : 파일 포인터를 매개변수로 받아 한 줄씩 읽어가며 공백을 기준으로 token을 잘라 비용 인접 행렬을 만드는 함수.
void getWeigth(struct Graph tmp_graph[]) : Graph 구조체 타입의 1차원 배열을 매개변수로 받아 비용 인접 행렬의 대각선을 기준으로 위쪽만 탐색하며, 그중 가중치가 의미 있는 경우에만 (가중치가 0이 아닌 양수인 경우) tmp_graph[]로 복사.
void initSet(int p[]) : 각각의 정점에 대해 집합을 만드는 함수. 이 프로그램에서는 parent[] 배열을 만들고 그 배열을 집합에 노드가 하나만 있다는 뜻인 –1로 초기화시키는 함수.
int find(int p[], int x, int y) : 정점 x와 y에 대해 각각의 최상위 노드를 찾고, 각각 어느 집합에 있는지 rootNode_x, rootNode_y에 저장하고, 두 노드가 같은 집합에 속해있는지를 리턴값으로 알려주는 함수.
붕괴법칙을 적용한 소스 코드에서는 이 단계에서 각각의 최상위 노드를 찾은 후 다시 최상위 노드까지 거슬러 올라가며 그 경로에 있는 노드들이 가지고 있는 부모 노드의 정보를 해당 집합의 최상위 노드의 인덱스로 변경해주는 작업 추가. -> 다음 find() 할 때 다시 거슬러 올라가지 않아도 됨.
void unionSet(int x, int y, int p[]) : 정점 x의 집합 크기와 정점 y의 집합 크기를 비교하여, 정점 x의 집합 크기가 정점 y의 집합 크기보다 크거나 같으면 정점 y의 집합을 정점 x의 집합으로 병합하고, 정점 y의 집합 크기가 정점 x의 집합 크기보다 크면 정점 x의 집합을 정점 y의 집합으로 병합하는 함수. 그리고 병합당한 집합(집합의 크기가 더 작은 집합)의 최상위 노드가 병합한 집합(집합의 크기가 더 큰 집합)의 정점을 가리키도록 설정.
void kruskalAlgo(struct Graph sg[], int par[]) : 크러스컬 알고리즘을 구현한 함수.
인자로 구조체 Graph 타입의 1차원 배열과 parent[] 배열을 받음. 가중치를 추출하는 함수를 호출하고, qsort()를 이용해 1차원 배열을 가중치를 기준으로 정렬하고, find와 union을 하는 함수. 알고리즘 실행을 마치고 나면 parent[] 배열의 모든 원소를 출력해줌.
void show() 함수 : union을 하나 할 때마다 parent[] 배열의 현재 상태를 보여주는 함수.
시간을 많이 잡아먹어 현재 프로그램에서는 호출하는 부분을 주석으로 처리해 둠.
소스코드 :
붕괴법칙을 사용하지 않은 경우
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 | // 붕괴법칙을 적용하지 않은 크러스컬 알고리즘 구현 #include <stdio.h> #include <string.h> #include <stdlib.h> // qsort() 함수가 선언된 헤더 파일 #include <time.h> // 시간을 측정하기 위한 clock() 함수가 선언된 헤더 파일 // #define CLOCKS_PER_SEC 1000 -> time.h에 선언되어 있음 #define n 9 // 정점의 개수 int line_cnt=0; // 간선의 개수 int tot_wei=0; // 총 가중치 int rootNode_x; // 정점 x의 루트 노드 int rootNode_y; // 정점 y의 루트 노드 struct Graph { // 두개의 정점과 가중치를 저장하는 구조체 선언 int x; // 정점 x 에서 int y; // 정점 y 까지의 int wei; // 가중치 weight } graph[n][n]; // 비용 인접 행렬 생성을 위한 graph[][] // 오름차순으로 정렬하기 위한 함수 int compare(struct Graph *g1, struct Graph *g2) { // 오름차순으로 qsort()를 사용하기 위해 값을 비교하여 리턴하는 함수 // 첫 번째 매개변수가 더 크면 양수 반환 // 첫 번째 매개변수가 더 작으면 음수 반환 // 두 매개변수가 같으면 0 반환 if(g1->wei > g2->wei) return 1; else if(g1->wei < g2->wei) return -1; return 0; } // 입력 데이터를 읽어 비용인접행렬을 만드는 함수 void readFileMakeGraph(FILE *fp) { char buf[10], *ptr; // 입력 파일을 읽어 올 buf와 token을 저장할 포인터 ptr int num; // 토큰 값을 int형으로 저장하기 위한 변수 int count=0; // 입력 데이터에서 값을 분리하기 위한 변수 int i=0, j=0; // i=행, j=열 // graph의 원소를 전부 -1로 초기화 // -1은 무한대를 의미 memset(graph, -1, n*n*sizeof(struct Graph)); // 파일 포인터 fp를 이용해 한 줄씩 최대 buf의 size만큼 buf[]로 읽어옴 while( (fgets(buf, sizeof(buf), fp)) != NULL ) { // 입력 파일의 끝까지 반복 ptr = strtok(buf, " "); while(ptr != NULL) { // ptr이 NULL이 아니면 실행 num = atoi(ptr); switch(count++) { case 0: i = num; // 행 삽입 break; case 1: j = num; // 열 삽입 break; case 2: graph[i][j].wei = num; // i에서 j까지의 가중치 num; graph[i][j].x = i; // 정점 x graph[i][j].y = j; // 정점 y graph[j][i].wei = num; // j에서 i까지의 가중치 num; graph[j][i].x = i; // 정점 x graph[j][i].y = j; // 정점 y break; } ptr = strtok(NULL, " "); } count = 0; } for(i=0; i<=n; i++) // i행 i열의 가중치는 0 // 즉, 자기 자신으로의 가중치는 0 graph[i][i].wei = 0; } // 의미 있는 가중치만 추출해내는 함수 void getWeigth(struct Graph tmp_graph[]) { int i, j; for(i=0; i<n; i++) for(j=i+1; j<n; j++) // 비용 인접 행렬 대각선을 기준으로 위쪽만 탐색 if(graph[i][j].wei > 0) // graph[i][j]의 가중치가 의미 있는 경우에만 실행 tmp_graph[line_cnt++] = graph[i][j]; // sorted_graph[] 배열에 복사 } // parent 배열 초기화 함수 void initSet(int p[]) { for(int i=0; i < n; i++) p[i] = -1; // 각각 노드를 하나만 가지고 있는 배열로 초기화 } //정점 x와 y를 union 하는 함수 void unionSet(int x, int y, int p[]) { if(p[rootNode_x] <= p[rootNode_y]) { // p[rootNode_x] 집합의 원소가 더 많거나 같으면 실행 p[rootNode_x] += p[rootNode_y]; // p[rootNode_y]집합을 p[rootNode_x]집합으로 병합 // p[rootNode_y]는 index x를 가리킨다 // 즉 y의 기존 최상위 노드가 x를 가리킨다 p[rootNode_y] = x; } else { // p[rootNode_y] 집합의 원소가 더 많으면 실행 p[rootNode_y] += p[rootNode_x]; // p[rootNode_x]집합을 p[rootNode_y]집합으로 병합 // p[rootNode_x]는 index y를 가리킨다 // 즉 x의 기존 최상위 노드가 y를 가리킨다 p[rootNode_x] = y; } } // 최상위 부모 노드를 찾아 자신이 어느 집합에 있는지 확인 및 저장하고 // 두 노드가 같은 집합에 속해 있는지 알려주는 함수 int find(int p[], int x, int y) { if(p[x] == -1 && p[y] == -1) { // p[x]와 p[y]가 둘 다 -1이면 union 가능 rootNode_x = x; // x의 최상위 노드는 자기 자신 rootNode_y = y; // y의 최상위 노드는 자기 자신 return 1; } // p[x]와 p[y]가 둘 다 -1이 아니면 while(1) { if(p[x] < 0 && p[y] < 0) // p[x]와 p[y]의 원소 값이 0보다 작으면 최상위 노드이기 때문에 while문 탈출 break; else if(p[x] > -1 && p[y] > -1) { // 둘 다 최상위 노드가 아니면 x = p[x]; // 부모 노드의 부모 노드를 찾아가기 위함 y = p[y]; // 부모 노드의 부모 노드를 찾아가기 위함 } else if(p[x] > -1 && p[y] < 0) { // p[x]만 최상위 노드가 아닌 경우 x = p[x]; // 부모 노드의 부모 노드를 찾아가기 위함 } else if(p[x] < 0 && p[y] > -1){ // p[y]만 최상위 노드가 아닌 경우 y = p[y]; // 부모 노드의 부모 노드를 찾아가기 위함 } else { // 이도 저도 아니면 에러메시지 출력 후 프로그램 종료 printf("find() error..."); exit(1); } } // 둘 다 최상위 노드이면 같은 집합에 속해있는지 비교 if(p[x] == p[y] ) // 서로 같은 집합이면 return 0; // 같은 집합에 속해있기 때문에 union 불가 // 같은 집합에 속해있지 않기 때문에 union 가능 rootNode_x = x; // x의 최상위 노드값 저장 rootNode_y = y; // y의 최상위 노드값 저장 return 1; } void kruskalAlgo(struct Graph sg[], int par[]) { int i; int cnt=0; // 정점의 개수-1 만큼 union해야하는데 이때, 카운트 하기 위한 변수 getWeigth(sg); // 가중치 추출 qsort(sg, line_cnt, sizeof(struct Graph), compare); // c언어에서 제공하는 sort initSet(par); // parent 배열 초기화 for(i=0; cnt!=n-1; i++) { // cnt가 정점 개수-1이 될 때까지 반복 switch(find(par, sg[i].x, sg[i].y)) { // find() 함수 실행 case 0: // union 불가능 break; case 1: // union 가능 unionSet(sg[i].x, sg[i].y, par); printf("%d) %d에서 %d까지의 가중치 : %d\n", cnt+1, sg[i].x, sg[i].y, sg[i].wei); cnt++; // union 성공 tot_wei += sg[i].wei; // union에 성공했으면 가중치를 더함 // show(par); // union 할 떄마다 parent[] 배열 출력 break; default : // 이도 저도 아니면 에러메시지 출력 후 프로그램 종료 printf("algo error...\n"); exit(1); } } printf("\n"); for(i=0; i<n; i++) // parent[] 배열 포맷을 인덱스와 함께 출력 printf("par[%d]\t", i); printf("\n"); for(i=0; i<n; i++) // 각각의 parent[] 배열 원소를 출력 printf("%d\t", par[i]); printf("\n\n"); printf("총 가중치 : %d\n", tot_wei); // 총 가중치 출력 } void show(int pa[]) { // parent[] 배열의 원소들을 출력해주는 함수 int i; for(i=0; i<n; i++) // parent[] 배열 포맷을 인덱스와 함께 출력 printf("par[%d]\t", i); printf("\n"); for(i=0; i<n; i++) // 각각의 parent[] 배열 원소를 출력 printf("%d\t", pa[i]); printf("\n\n"); } int main() { clock_t start, finish; // 시간 측정을 위한 clock_t타입의 변수 선언 int i=0; int parent[n]; // 정점 개수 만큼의 원소를 가진 parent 배열 생성 struct Graph sorted_graph[200]; // 가중치를 뽑아내어 저장하고 정렬 할 구조체 배열 선언 FILE *fp = fopen("graphInf.txt", "r"); // 입력 데이터 텍스트 파일 오픈 if(!fp) { // 파일이 없을 경우 에러 메시지 출력 후 프로그램 종료 printf("입력 파일이 없습니다.\n"); return 0; } readFileMakeGraph(fp); // 비용인접행렬을 만드는 함수 호출 // clock() 함수는 millisecond(ms) 단위로 시간 반환 // 1ms = 1/1000sec start = clock(); // 시작 지점에서 시간 체크 kruskalAlgo(sorted_graph, parent); // 크러스컬 알고리즘 실행 finish = clock(); // 종료 지점에서 시간 체크 printf("프로그램 실행시간 : %fs\n", (float)(finish-start)/CLOCKS_PER_SEC); // (종료 시간 - 시작 시간)/1000 = 측정 구간 실행 시간 return 0; } |
'Algorithm' 카테고리의 다른 글
| 크러스컬 알고리즘 구현 2 (붕괴법칙을 적용한 방법) (3) | 2021.04.09 |
|---|---|
| 크러스컬(Kruskal) 알고리즘 (1) | 2020.07.02 |
| 합병 정렬(Merge Sort) 알고리즘 (1) | 2020.03.18 |
| 삽입 정렬(Insertion Sort) 알고리즘 (1) | 2020.03.17 |




